Моделирование произвольного импеданса нагрузки в LTspice

При моделировании в LTspice согласующих устройств, трансформаторов и многих других схем часто требуется иметь возможность задать произвольный импеданс нагрузки в виде R + jX, где R – активная составляющая импеданса, а X – реактивная. Готового элемента, которому можно было бы просто назначить требуемый нам импеданс, в библиотеке LTspice нет. Решение задачи «в лоб» тривиально: берем резистор с сопротивлением R и в зависимости от знака реактивной составляющей, подключаем к нему последовательно либо конденсатор, либо катушку индуктивности такого номинала, чтобы получить требуемое значение X на заданной частоте. Это решение можно даже красиво параметризовать, например так, как показано на схеме ниже:

Параметрическая частотно-зависимая нагрузка

Скачать схему

Давайте разберемся с тем, как это работает. Сначала мы задаем нужный нам импеданс и частоту:

.param R = 50       ; активная составляющая импеданса
.param X = 100      ; реактивная составляющая импеданса
.param F = 10Meg    ; частота

В нашем примере импеданс равен 50 + 100j Ом на частоте 10 МГц. Значение R может быть любым кроме нуля, иначе LTspice огорчится и выдаст сообщение об ошибке. Значение R также может быть отрицательным, если это зачем-то нужно для анализа схемы. Если требуется чисто реактивный импеданс, можно либо задать значение R очень малым (например, 1e-15 Ом), либо просто исключить резистор из схемы. Значение X может быть любым.

Далее, преобразовываем циклическую частоту в круговую, которая потом будет использована для вычисления емкости и индуктивности:

.param omega  = 2 * pi * F

Затем, рассчитываем значения емкости и индуктивности. Если X отрицателен, то в качестве реактивного элемента будет использован конденсатор, если положителен, то катушка индуктивности, а если X равен нулю, то номиналы обоих элементов будут выбраны так, чтобы они не оказывали влияния на работу схемы:

.param C = if(X < 0, 1 / (omega * abs(X)), 1)
.param L = if(X > 0, X / omega, 0)

Значения емкости и индуктивности рассчитываются по следующим формулам:

$C = \frac{1}{\omega X}\;\;\;\;L = \frac{X}{\omega}\;\;\;\;\omega = 2*\pi*F$

Номинал неиспользуемого конденсатора следует выбрать достаточно большим, чтобы он не оказывал влияния на работу схемы во всем диапазоне частот, но при этом не слишком большим, иначе на этапе симуляции могут возникнуть ошибки. 1 фарад является подходящим выбором. Номинал неиспользуемой катушки индуктивности можно установить равным нулю.

В старых версиях LTspice оператор if не поддерживал логические выражения при работе внутри директивы .param. В свежих версиях это поправили, однако документация на LTspice до сих пор содержит устаревшее описание. Раньше выражения для емкости и индуктивности должны были бы выглядеть как-то так:

.param C = if(limit(X, -0.5, 0.5)+0.5, 1, 1 / (omega * abs(X)))
.param L = if(limit(X, -0.5, 0.5)+0.5, X / omega, 0)

Примечание: иногда бывает удобно в режиме временного анализа задать время симуляции таким, чтобы наблюдать определенное количество периодов исследуемого сигнала. Вот как можно это сделать:

.param T = 1 / F * 10
.tran {T}

В первой строке рассчитывается временной интервал T, соответствующий десяти периодам сигнала на частоте F. Вторая строка выполняет симуляцию длительностью T.

В этой статье мы будем использовать симуляцию в частотной области, так как её результаты более наглядны:

.ac lin 1k 1Meg 30Meg
.net V1

Выполним частотный анализ с количеством точек равным 1000 в диапазоне от 1 до 30 МГц. Кроме этого, с помощью директивы .net рассчитаем получившийся импеданс. Результаты симуляции приведены ниже:

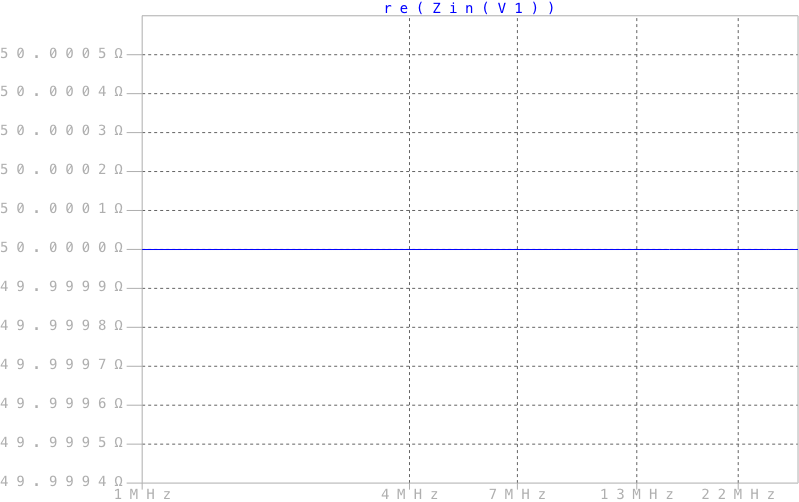График активной составляющей импеданса

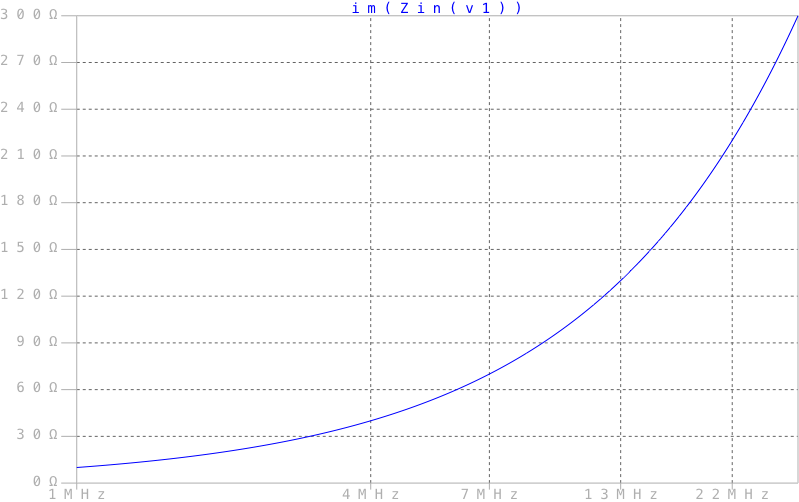График реактивной составляющей импеданса

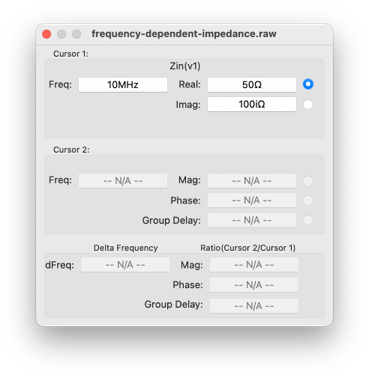Импеданс на частоте 10 МГц

Из результатов видно, что на частоте 10 МГц нагрузка имеет импеданс 50 + 100j Ом, как нам и требовалось. Также видно, что реактивная составляющая импеданса меняется в зависимости от частоты.

Такой метод моделирования произвольного импеданса нагрузки хорошо работает как в режиме частотного, так и в режиме временного анализа, является простым и интуитивно понятным. Однако требуемый импеданс такая нагрузка имеет только на одной заданной частоте, что не всегда оказывается удобным. Иногда удобнее иметь нагрузку, импеданс которой остается постоянным вне зависимости от частоты. Например, это бывает полезно при исследовании работы трансформаторов.

К сожалению, схема выше никак не может быть преобразована так, чтобы ее импеданс оставался постоянным при изменении частоты. Это потребовало бы изменять номиналы конденсатора и катушки индуктивности непосредственно во время симуляции и рассчитывать их исходя из некоторой текущей частоты, что невозможно сделать в LTspice. Тем не менее, в LTspice все же есть подходящий нам инструмент, который позволит решить задачу. Этим инструментом является преобразование Лапласа.

Если в этот момент вам стало грустно, то сразу хочу предупредить, пугаться не стоит, никакой сложной математики в статье не будет. О том, что такое на самом деле преобразование Лапласа, какими замечательными свойствами оно обладает и почему находит широкое применение в математике и физике лучше всего почитать в специализированной литературе. Здесь же я сосредоточусь исключительно на использовании преобразования Лапласа в LTspice.

Итак, в LTspice для ряда элементов можно задать функцию принимающую в качестве входного параметра комплексную частоту $s = \sigma + j\omega$ и возвращающую комплексное число, на которое будет умножен либо номинал элемента, либо значение его передаточной функции. О том, что такое комплексная частота можно почитать в отдельной заметке. Сейчас важно знать две вещи: во-первых, в LTspice $\sigma$ всегда равна нулю, то есть, по сути, на вход преобразования Лапласа подается угловая частота $\omega = 2\pi f$, умноженная на мнимую единицу. Получить действительное значение $\omega$ можно с помощью выражения abs(s). Во-вторых, поскольку мы собрались делать частотно-независимую нагрузку, то и $\omega$ нам ни зачем не нужна, ведь результат преобразования Лапласа не должен зависеть от частоты.

Согласно документации на LTspice, преобразование Лапласа можно задать для следующих элементов:

• Arbitrary Behavioral Voltage or Current Sources (BI, BV);
• Voltage Dependent Voltage Source;
• Voltage Dependent Current Source;

Кроме этого, известно, что преобразование Лапласа можно задать для резисторов, хотя в документации на LTspice об этом ничего не сказано. С резисторами есть одна особенность: преобразование Лапласа используется не для расчета значения сопротивления, как можно было бы подумать, а для расчета проводимости, что создает некоторую путаницу. Напоследок, отсутствие упоминания этой возможности в документации оставляет ощущение легкой неуверенности в том, что в нужный момент все будет работать как надо, хотя на первый взгляд все работает. С другой стороны, у резистора крайне подходящее по смыслу условное графическое обозначение.

Из элементов, официально поддерживающих преобразование Лапласа, для целей создания нагрузки с частотно-независимым импедансом мне больше всего нравится использовать Arbitrary Behavioral Voltage Source (источник напряжения с произвольным поведением). Это не единственный возможный выбор, но один из самых простых и удобных.

Для того чтобы не раздувать и без того немаленькую статью, давайте сделаем нагрузки с произвольным частотно-независимым импедансом из резистора и источника напряжения с произвольным поведением. Эксперименты с остальными элементами любознательный читатель может провести сам.

Схема с резистором выглядит так:

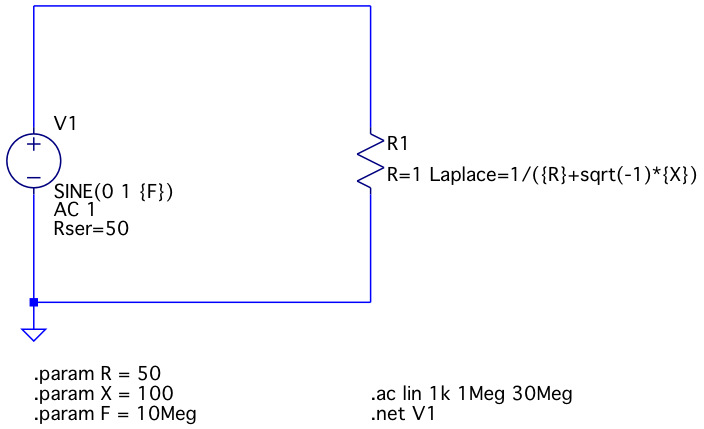Частотно-независимая нагрузка, вариант с резистором

Скачать схему

При симуляции схемы LTspice преобразует значение сопротивления резистора R1 в комплексную проводимость, а затем умножает на результат вычисления преобразования Лапласа. Фактически выполняются следующие вычисления: $Y = \frac{1}{R1}\cdot\frac{1}{R + jX}$ Так как значение сопротивления R1 равно одному Ому, первый сомножитель равен единице, поэтому полная проводимость равна $Y = \frac{1}{R + jX}$ что эквивалентно импедансу R + jX.

sqrt(-1) используется в качестве способа задать в преобразовании Лапласа мнимую единицу, поскольку в LTspice отсутствует специальная константа для этого.

Результаты симуляции приведены ниже:

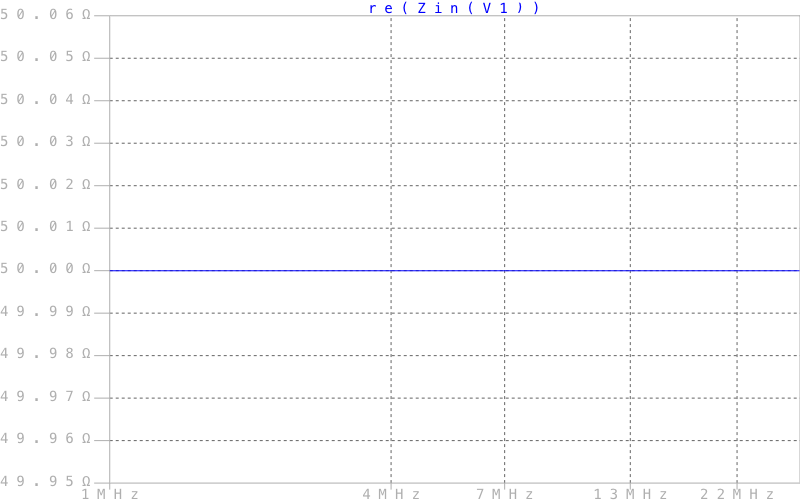График активной составляющей импеданса

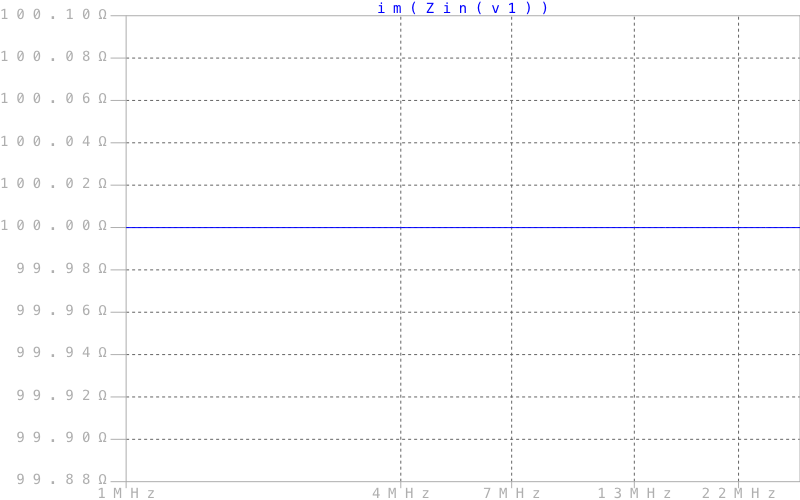График реактивной составляющей импеданса

Из графиков видно, что импеданс нагрузки равен 50 + 100j Ом и не зависит от частоты, что нам и требовалось.

Схема с источником напряжения с произвольным поведением выглядит так:

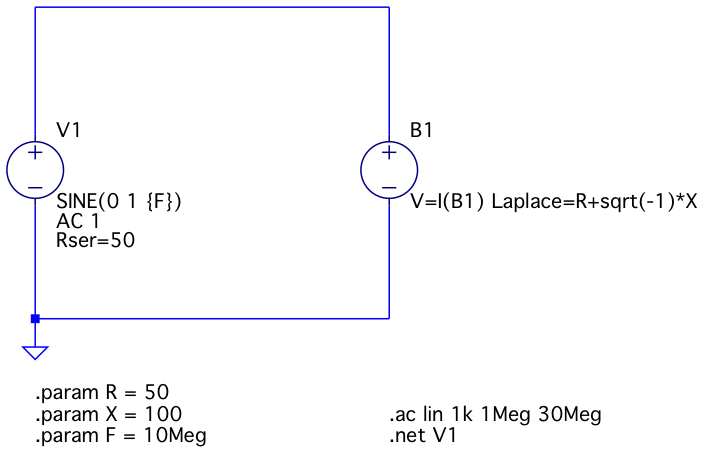Частотно-независимая нагрузка, вариант с источником напряжения с произвольным поведением

Скачать схему

Функция, определяющая поведение источника напряжения B1, задана как V=I(B1). Другими словами, напряжение на клеммах источника равно току через него. Это эквивалентно резистору номиналом 1 Ом. Далее, получившееся значение напряжение умножается на результат преобразования Лапласа, который и определяет итоговый импеданс.

Обратите внимание, что параметры R и X в преобразовании Лапласа заданы без фигурных скобок в отличие от схемы с резистором. Такой синтаксис является правильным в данном случае.

Графики получившегося импеданса приводить не буду, так как они эквивалентны графикам для варианта схемы с резистором.

Преобразование Лапласа в LTspice хорошо работает при анализе в частотной области и несколько хуже при анализе во временной области. Эта тема подробно раскрыта в документации на LTspice, см. описание Arbitrary Behavioral Voltage or Current Sources.

Мы разобрались с тем, как в LTspice можно моделировать произвольный импеданс нагрузки, научились делать его частотно-независимым и узнали о некоторых тонкостях работы с симулятором. В следующих статьях мы будем использовать эти знания для моделирования работы тех или иных устройств.