Что такое комплексная частота

Кроме привычного нам понятия частоты, которая бывает циклической и угловой, в электротехнике также иногда применяется понятие комплексной частоты. Давайте разберемся с тем, что оно обозначает и какой у него физический смысл.

Циклическая и угловая частота говорят нам о том, насколько быстро изменяется фаза некоторого колебательного процесса. Понятие комплексной частоты добавляет к этому информацию о том, насколько быстро нарастает или затухает амплитуда этого колебательного процесса.

Комплексная частота обычно обозначается символом $s$ записывается в виде: $s = \sigma + j\omega$ где $\sigma$ – постоянная времени изменения амплитуды колебательного процесса, $\omega$ – угловая частота равная $2\pi f$, а $j$ – мнимая единица.

Для того чтобы понять как это работает, возьмем функцию: $f(t) = e^{st}$ где e - основание натурального логарифма, $s$ - комплексная частота, а $t$ - время. При этом время может изменяться от нуля до бесконечности.

Заменим $s$ в формуле выше его определением и раскроем скобки: $f(t) = e^{(\sigma + j\omega)t} = e^{\sigma t + j\omega t}$

Согласно правилу умножения степеней, это выражение можно переписать следующим образом: $f(t) = e^{\sigma t} e^{j\omega t}$

Первый сомножитель, $e^{\sigma t}$ – это обычная экспоненциальная функция. Если $\sigma$ положительна, то значение сомножителя нарастает при увеличении $t$, если отрицательна, то убывает, а если $\sigma = 0$, то значение сомножителя остается постоянным и равным 1, так как $e^{0 * t} = e^{0} = 1$. Это имеет физический смысл экспоненциально нарастающей, убывающей или остающейся постоянной амплитуды колебательного процесса.

Для наглядности, давайте построим график экспоненциальной функции $f(t) = e^{\sigma t}$ при $\sigma = -0.5$:

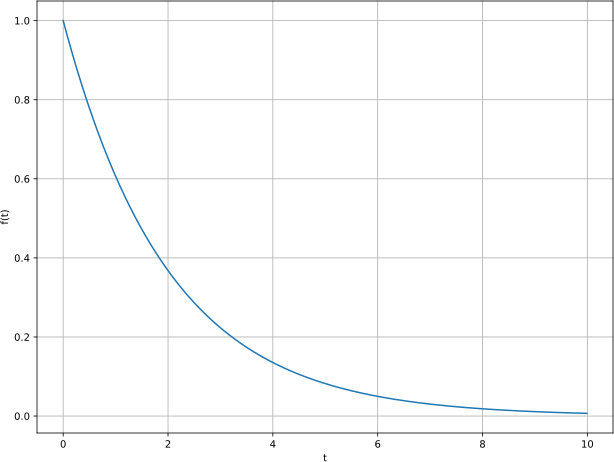График функции $f(x) = e^{-0.5t}$

Из графика видно, что функция убывает по мере роста $t$ в $e$ раз за каждые $2t$.

Теперь давайте разберемся со вторым сомножителем $e^{j\omega t}$. Для того чтобы понять, что он обозначает надо вспомнить формулу Эйлера, которая связывает комплексную экспоненту с тригонометрическими функциями: $e^{jx} = \cos(x) + j\sin(x)$ Это позволит нам переписать сомножитель $e^{j\omega t}$ в виде: $e^{j\omega t} = \cos(\omega t) + j\sin(\omega t)$ И мы немедленно увидим в формуле выше гармонические колебания единичной амплитуды, имеющие нулевую начальную фазу и происходящие с частотой $\omega$.

Для простоты, давайте сосредоточимся на действительной части выражения: $Re(e^{j\omega t}) = cos(\omega t)$ и далее будем использовать только её.

Построим график функции $f(t) = \cos(\omega t)$ при $\omega = 2\pi f$ и $f = 2$:

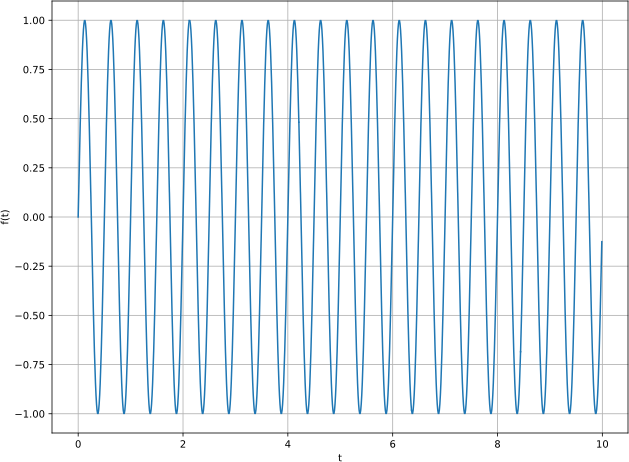График функции $f(t) = \cos(\omega t)$

На графике видны обычные гармонические колебания.

Наконец, перемножим сомножители $e^{\sigma t}$ и $Re(e^{j\omega t})$: $f(t) = e^{\sigma t} Re(e^{j\omega t}) = e^{\sigma t}\cos(\omega t)$ и построим график получившейся функции при $\sigma = -0.5$, $\omega = 2\pi f$ и $f = 2$:

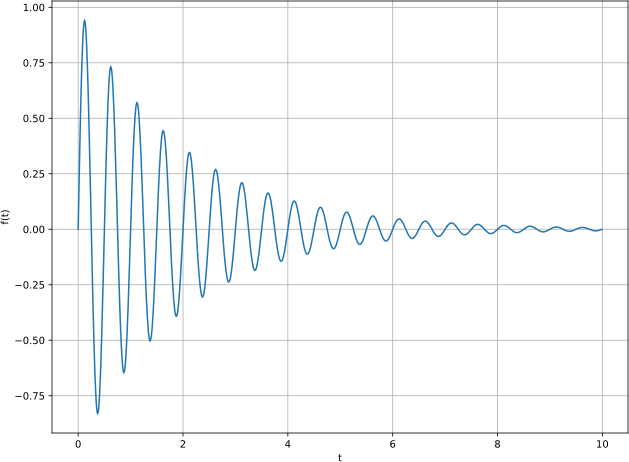График функции $f(t) = e^{\sigma t}\cos(\omega t)$

На графике видно экспоненциально затухающие гармонические колебания.

Итак, мы разобрались, что комплексная частота $s = \sigma + j\omega$ – это всего лишь способ описать гармонические колебания имеющие частоту $\omega$ и изменяющие свою амплитуду по экспоненциальному закону с постоянной времени $\sigma$.

Концепция комплексной частоты применяется в преобразовании Лапласа, очень мощном инструменте анализа используемом в математике и физике. Преобразование Лапласа также часто применяют при анализе и моделировании электронных схем. Например, с ним могут работать такие хорошо известные радиолюбителям программы как LTspice и MMANA.